At Oslandia, we like working with Open Source tool projects and handling Open (geospatial) Data. In this article series, we will play with the OpenStreetMap (OSM) map and subsequent data. Here comes the sixth article of this series, dedicated to user metadata normalization.
1 Let’s remind the user metadata
After the previous blog post, we got a set of features aiming to describe how OSM users contribute to the mapping effort. That will be our raw materials towards the clustering process. If we saved the user metadata in a dedicated .csv file, it can be recovered easily:
import pandas as pd user_md = pd.read_csv("../src/data/output-extracts/bordeaux-metropole/bordeaux-metropole-user-md-extra.csv", index_col=0) user_md.query('uid == 24664').T
uid 24664 lifespan 2449.000000 n_inscription_days 3318.000000 n_activity_days 35.000000 n_chgset 69.000000 dmean_chgset 0.000000 nmean_modif_byelem 1.587121 n_total_modif 1676.000000 n_total_modif_node 1173.000000 n_total_modif_way 397.000000 n_total_modif_relation 106.000000 n_node_modif 1173.000000 n_node_modif_cr 597.000000 n_node_modif_imp 360.000000 n_node_modif_del 216.000000 n_node_modif_utd 294.000000 n_node_modif_cor 544.000000 n_node_modif_autocor 335.000000 n_way_modif 397.000000 n_way_modif_cr 96.000000 n_way_modif_imp 258.000000 n_way_modif_del 43.000000 n_way_modif_utd 65.000000 n_way_modif_cor 152.000000 n_way_modif_autocor 180.000000 n_relation_modif 106.000000 n_relation_modif_cr 8.000000 n_relation_modif_imp 98.000000 n_relation_modif_del 0.000000 n_relation_modif_utd 2.000000 n_relation_modif_cor 15.000000 n_relation_modif_autocor 89.000000 n_total_chgset 153.000000 p_local_chgset 0.450980 n_total_chgset_id 55.000000 n_total_chgset_josm 0.000000 n_total_chgset_maps.me_android 0.000000 n_total_chgset_maps.me_ios 0.000000 n_total_chgset_other 1.000000 n_total_chgset_potlatch 57.000000 n_total_chgset_unknown 40.000000
Hum… It seems that some unknown features have been added in this table, isn’t it?
Well yes! We had some more variables to make the analysis finer. We propose you to focus on the total number of changesets that each user has opened, and the corresponding ratio between changeset amount around Bordeaux and this quantity. Then we studied the editors each user have used: JOSM? iD? Potlatch? Maps.me? Another one? Maybe this will give a useful extra-information to design user groups.
As a total, we have 40 features that describe user behavior, and 2073 users.
2 Feature normalization
2.1 It’s normal not to be Gaussian!
We plan to reduce the number of variables, to keep the analysis readable and interpretable; and run a k-means clustering to group similar users together.
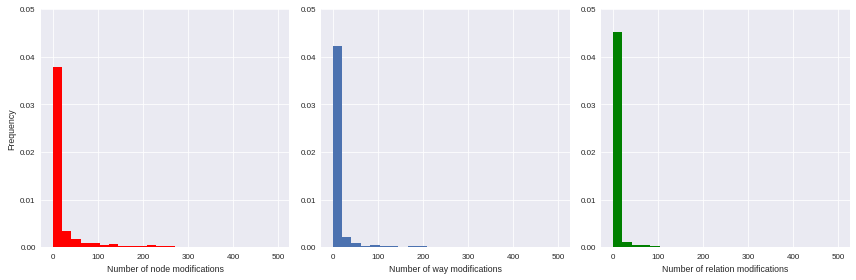
Unfortunately we can’t proceed directly to such machine learning procedures: they work better with unskewed features (e.g. gaussian-distributed ones) as input. As illustrated by the following histograms, focused on some available features, the variables we have gathered are highly left-skewed (they seems exponentially-distributed, by the way); that leading us to consider an alternative normalization scheme.
import matplotlib.pyplot as plt import seaborn as sns import numpy as np %matplotlib inline f, ax = plt.subplots(1,3, figsize=(12,4)) ax[0].hist(user_md.n_node_modif, bins=np.linspace(0,500, 25), color='r', normed=True) ax[0].set_xlabel('Number of node modifications') ax[0].set_ylabel('Frequency') ax[0].set_ylim(0,0.05) ax[1].hist(user_md.n_way_modif, bins=np.linspace(0,500, 25), normed=True) ax[1].set_xlabel('Number of way modifications') ax[1].set_ylim(0,0.05) ax[2].hist(user_md.n_relation_modif, bins=np.linspace(0,500, 25), color='g', normed=True) ax[2].set_xlabel('Number of relation modifications') ax[2].set_ylim(0,0.05) plt.tight_layout() sns.set_context("paper")
2.2 Feature engineering
The basic idea we want you to keep in mind is the following one: if we find some mathematical tricks to express our variables between simple bounds (e.g. 0 and 100, or -1 and 1), we could design a smarter representation of user characteristics.
First of all you should notice that a lot of variables can be expressed as percentages of other variables:
- the number of node/way/relation modifications amongst all modifications;
- the number of created/improved/deleted elements amongst all modifications, for each element type;
- the number of changesets opened with a given editor, amongst all changesets.
def normalize_features(metadata, total_column): transformed_columns = metadata.columns[metadata.columns.to_series() .str.contains(total_column)] metadata[transformed_columns[1:]] = metadata[transformed_columns].apply(lambda x: (x[1:]/x[0]).fillna(0), axis=1) normalize_features(user_md, 'n_total_modif') normalize_features(user_md, 'n_node_modif') normalize_features(user_md, 'n_way_modif') normalize_features(user_md, 'n_relation_modif') normalize_features(user_md, 'n_total_chgset')
Other features can be normalized starting from their definition: we know that lifespan and n_inscription_days can’t be larger than the OSM lifespan itself (we consider the OSM lifespan as the difference between the first year of modification within the area and the extraction date).
timehorizon = (pd.Timestamp("2017-02-19") - pd.Timestamp("2007-01-01"))/pd.Timedelta('1d') user_md['lifespan'] = user_md['lifespan'] / timehorizon user_md['n_inscription_days'] = user_md['n_inscription_days'] / timehorizon
Finally we have to consider the remaining variables that can’t be normalized as percentages of other variables, or as percentages of meaningful quantities. How can we treat them?
We choose to transform these features by comparing users to any other: knowing that a user did 100 modifications is interesting, however we could also compare it with other users, e.g. by answering the question « how many users did less modifications? ». That’s typically the definition of the empirical cumulative distribution function.
import statsmodels.api as sm def ecdf_transform(metadata, feature): ecdf = sm.distributions.ECDF(metadata[feature]) metadata[feature] = ecdf(metadata[feature]) new_feature_name = 'u_' + feature.split('_', 1)[1] return metadata.rename(columns={feature: new_feature_name}) user_md = ecdf_transform(user_md, 'n_activity_days') user_md = ecdf_transform(user_md, 'n_chgset') user_md = ecdf_transform(user_md, 'nmean_modif_byelem') user_md = ecdf_transform(user_md, 'n_total_modif') user_md = ecdf_transform(user_md, 'n_node_modif') user_md = ecdf_transform(user_md, 'n_way_modif') user_md = ecdf_transform(user_md, 'n_relation_modif') user_md = ecdf_transform(user_md, 'n_total_chgset')
Consequently we can characterize a user with such new dashboard:
user_md.query("uid == 24664").T
uid 24664 lifespan 0.661534 n_inscription_days 0.896272 u_activity_days 0.971539 u_chgset 0.969609 dmean_chgset 0.000000 u_modif_byelem 0.838881 u_total_modif 0.966715 n_total_modif_node 0.699881 n_total_modif_way 0.236874 n_total_modif_relation 0.063246 u_node_modif 0.967680 n_node_modif_cr 0.508951 n_node_modif_imp 0.306905 n_node_modif_del 0.184143 n_node_modif_utd 0.250639 n_node_modif_cor 0.463768 n_node_modif_autocor 0.285592 u_way_modif 0.971539 n_way_modif_cr 0.241814 n_way_modif_imp 0.649874 n_way_modif_del 0.108312 n_way_modif_utd 0.163728 n_way_modif_cor 0.382872 n_way_modif_autocor 0.453401 u_relation_modif 0.984563 n_relation_modif_cr 0.075472 n_relation_modif_imp 0.924528 n_relation_modif_del 0.000000 n_relation_modif_utd 0.018868 n_relation_modif_cor 0.141509 n_relation_modif_autocor 0.839623 u_total_chgset 0.485769 p_local_chgset 0.450980 n_total_chgset_id 0.359477 n_total_chgset_josm 0.000000 n_total_chgset_maps.me_android 0.000000 n_total_chgset_maps.me_ios 0.000000 n_total_chgset_other 0.006536 n_total_chgset_potlatch 0.372549 n_total_chgset_unknown 0.261438
We then know that the user with ID 24664 did more node, way and relation modifications than respectively 96.7, 97.2 and 98.5% of other users, or that amongst his node modifications, 50.9% were creations, and so on…
In order to complete the normalization procedure, we add a final step that consists in scaling the features, to ensure that all of them have the same min and max values. As the features are still skewed, we do it according to a simple Min-Max rule, so as to avoid too much distorsion of our data:
from sklearn.preprocessing import RobustScaler scaler = RobustScaler(quantile_range=(0.0, 100.0)) # = Min-max scaler X = scaler.fit_transform(user_md.values)
3 Conclusion
This post shows you the work involved in machine learning procedure preparation. It seems quite short, however it represents a long long and unavoidable process with several try-and-error iteration loops to let the data do the talking (even an exciting job like data scientist has its dark side…)! We will exploit these new data in some machine learning procedures in the next post, dedicated to the user classification.