
À la suite d’un premier article dédié à la présentation du projet Univers, il est temps d’entrer dans les détails techniques, entre données 3D et mathématiques, jusqu’à notre premier algorithme de machine learning !
TL;DR
La donnée initiale est un ensemble de tableaux XYZ(RGB), sans information sémantique. L’implémentation d’algorithmes supervisés est donc impossible, et il est nécessaire d’analyser les propriétés géométriques de la donnée 3D. Ici, deux étapes sont nécessaires pour réaliser ce travail :
- indexer le nuage de points via une méthode telle que le kd-tree, pour constituer des voisinages locaux centrés sur chacun des points du nuage ;
- exécuter des Analyses en Composantes Principales (ACP) pour chaque voisinage de manière à caractériser chaque point.
À la suite du calcul des ACP, on obtient un ensemble de variables décrivant tous les points. Un algorithme de clustering standard (à l’image des k-means) peut être exécuté pour ranger chaque point dans une classe sémantique, sans aucune connaissance préalable relative à la nature du nuage.
La donnée 3D
Au départ du projet, Géolithe nous a fourni un ensemble de scènes 3D au format .las. Ce standard de stockage contient des informations relatives à la localisation (coordonnées x, y et z) et à d’autres aspects (couleurs, classification sémantique) d’une part, mais également des métadonnées d’autre part.
Dans notre cas, les fichiers .las, construits par photogrammétrie et lasergrammétrie, contenaient les variables XYZ pour la localisation, RGB pour la couleur…et c’est à peu près tout. La figure ci-dessous illustre le type de jeu de données que nous avons eu à traiter, où devaient être identifiées des surfaces telles que la végétation, les falaises, les éboulements, la route ou encore les infrastructures diverses.

Exemples de jeux de données utilisés lors de ce projet
Lire les données avec Python est très simple via la bibliothèque laspy. Ceci étant dit, la tâche de visualisation est plus complexe, et nécessite des outils dédiés (e.g. CloudCompare), dans la mesure où ces jeux de données contiennent un très grand nombre de points (entre 600k et 32M).
Analyser les propriétés géométriques de la donnée
Notre premier objectif était l’implémentation d’un algorithme de Deep Learning pour la segmentation sémantique des nuages de points 3D (un problème de classification, beaucoup de données, tout ça semblait pertinent, n’est-ce pas ?). Cependant, nous avons vite dû revenir à quelque chose de beaucoup plus pragmatique en l’absence d’annotations sur les nuages de points : qui dit pas de base d’apprentissage, dit aussi pas d’entraînement de modèle prédictif…
Les sections suivantes reprennent le processus engagé pour enrichir la base d’information disponible.
Indexation du nuage de points
En premier lieu, le nuage de points doit être indexé à l’aide d’un algorithme de partitionnement, pour pouvoir construire de manière la plus efficace possible des voisinages locaux autour de chacun des points. Nous avons choisi la méthode du kd-tree pour ce faire, et son implémentation en Python via la bibliothèque scipy. Obtenir un voisinage local se fait comme suit :
from scipy.spatial import KDTree
point_cloud = ... # Importer le jeu de données 3D (comme un numpy.array)
# Construire l'arbre de recherche
tree = scipy.spatial.KDTree(point_cloud, leaf_size=1000)
point = point_cloud[0] # Sélectionner un point quelconque dans le nuage
# Récupérer ses k plus proches voisins à partir de l'arbre de recherche
dist_to_neighbors, neighbor_indices = tree.query(point, k)
neighborhoods = point_cloud[neighbor_indices]
Exécuter des ACP (beaucoup d’ACP)
Le voisinage local de chaque point est obtenu par l’indexation décrite précédemment. À ce stade, aller plus loin dans l’analyse est synonyme d’étude de la structure interne de chaque voisinage.
En exécutant des Analyses en Composantes Principales (ACP) sur un voisinage local, on peut savoir s’il s’organise selon un axe 1D, un plan 2D ou un espace en 3D : le voisinage ressemble-t-il à un arbre, un mur, ou est-il bruité dans l’espace 3D ? Dans le contexte d’environnement naturel, on fait l’hypothèse que la végétation ou une falaise n’ont pas la même structure interne !
Comme suggéré par l’outil CANUPO 1, la taille du voisinage a aussi un impact sur la structure locale (quelle pertinence a la description d’un arbre avec 20 points ? 200 ? 2000 ?). Considérer un panel de plusieurs tailles distinctes peut ainsi grandement améliorer la représentation des zones.
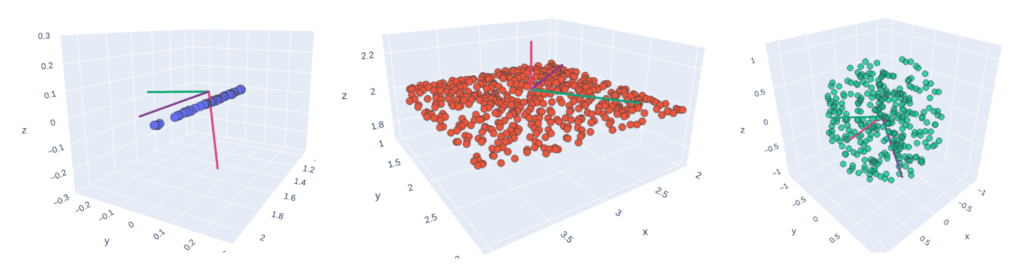
Vecteurs propres après ACP, sur des nuages de points canoniques 1, 2 et 3D
En Python, la bibliothèque scikit-learn est ici un outil incontournable. En outre, comme il s’agit d’exécuter un très grand nombre d’ACP (n*p, où n est le nombre de points, et p le nombre de tailles de voisinage), une attention particulière doit être portée au temps de calcul, pour rester dans des standards acceptables du point de vue industriel. La parallélisation (paquet multiprocessing) est ainsi incontournable (et ça pourrait faire l’objet d’un article de blog à part entière !).
Informations géométriques pour décrire un point
Après l’exécution des ACP sur les voisinages locaux, un grand ensemble de variables peuvent être déduites des valeurs propres obtenues. Cet article n’a pas vocation à les lister toutes, cependant une taxonomie brève est donnée ici, qui s’appuie notamment sur 2 :
- Les features géométriques 3D, déduites d’ACP à trois dimensions : coordonnées barycentriques (d’après 1), changement de courbure, coefficient de linéarité, de planarité, anisotropie, … ;
- Les features géométriques 2D, déduites d’ACP à deux dimensions (des informations supplémentaires peuvent être déduites d’une simple projection sur un plan) ;
- Propriétés 2D/3D intrinsèques, qui ne sont d’ailleurs pas issues d’une ACP : densité de point dans le voisinage, variabilité de la composante verticale z, … ;
- Variables additionnelles issues de définitions alternatives du voisinage : maillage en grille plutôt que via un kd-tree, et calcul de valeurs à l’échelle de chaque maille.
Les valeurs de l’ensemble des variables ainsi constitué correspondent en quelque sorte à la « carte d’identité » de chaque point.
Classer les points en fonction de leurs propriétés géométriques
À ce stade, nous avons un ensemble de N points, décrits par M variables. Il est possible de les grouper en fonction des valeurs de ces variables, en admettant que ces groupes seront autant de types sémantiques liés aux surfaces de terrain.
Cette description renvoie directement aux algorithmes de clustering. Là encore, scikit-learn est utilisé dans l’implémentation Python, et donne les résultats suivants sur les exemples de jeux de données présentés plus haut, sans grand effort de normalisation ou de feature engineering :

Scènes 3D après clusterisation
Si on compare ces résultats avec les scènes brutes, on voit que les conclusions sont très sensibles aux scènes elles-mêmes :
- Les surfaces dans la scène de gauche (600k points, 3 clusters, 40*50*50 mètres) sont plutôt bien modélisées, avec de la végétation sur le haut de l’image, la falaise au centre, et des éboulis sur le bas.
- Le second exemple (1.2M points, 3 clusters, 40*50*30) présente une route situé sur les contreforts d’une falaise. L’algorithme détecte ces zones, dans les grandes lignes. Mais l’information reste grossière, et nécessite un retraitement a posteriori.
- Dans le troisième exemple, la scène est plus volumineuse (9.8M points, 4 clusters, 610*690*360 mètres), les types de surface plus dispersés dans la scène. Les résultats produits par le k-mean sont de moins bonne qualité.
Conclusion
Quand l’information sémantique n’est pas disponible avec la donnée 3D, il est toujours possible de l’inférer à partir de la structure géométrique du nuage de points.
Le processus décrit ici produit des résultats convaincants, pour peu que les scènes 3D associées restent simples (peu de classes, échelle réduite). Pour traiter des cas plus complexes, ou obtenir des résultats plus séduisants, investir dans une phase d’annotation, même réduite, semble inévitable ; le paradigme évoluant au profit d’approches supervisées, ce sera l’objet du troisième et dernier article de la série consacrée à cette thématique.
N’hésitez pas à commenter l’article, ou à nous contacter (infos@oslandia.com) en cas de question ou de remarque vis-à-vis de la méthodologie décrite ici !
1 Nicolas Brodu, Dimitri Lague, 2011. [3D Terrestrial lidar data classification of complex natural scenes using a multi-scale dimensionality criterion: applications in geomorphology](https://arxiv.org/abs/1107.0550). arXiv:1107.0550.
2 Martin Weinmann, Boris Jutzi, Stefan Hinz, Clément Mallet, 2015. [Semantic point cloud interpretation based on optimal neighborhoods, relevant features and efficient classifiers](http://recherche.ign.fr/labos/matis/pdf/articles_revues/2015/isprs_wjhm_15.pdf). ISPRS Journal of Photogrammetry and Remote Sensing, vol 105, pp 286-304.


