Résoudre des équations graphiquement avec PostGIS

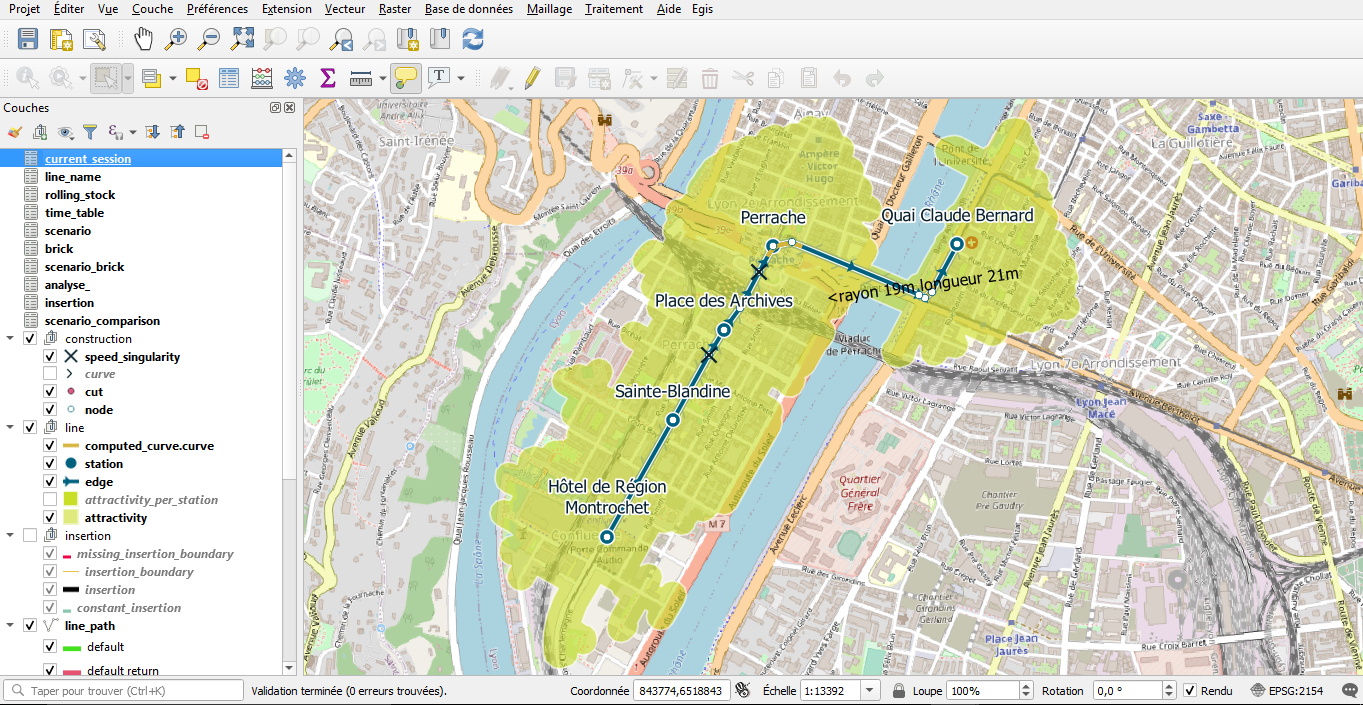
Oslandia accompagne la Direction de Etudes Amont et de l’Innovation (DEAI) d’Egis Rail dans la refonte et l’intégration de ses outils métier.

L’objectif est de disposer, en phase faisabilité de conception des lignes de transport en commun, d’une application web permettant :

• de tracer des lignes de transport en commun sur un fond de plan,
• d’étudier l’impact des lignes en matière de population desservie,
• d’estimer leurs coûts de réalisation et d’exploitation.

Ces besoins sont à ce jour remplis par des SIG bureautiques, des outils spécialisés (par exemple calcul d’isochrone piétons) et des outils métier développés en interne.

La solution en cours de réalisation s’appuie sur une base de données PostGIS en utilisant pleinement sa richesse fonctionnelle pour intégrer les traitements au modèle de données.

Cette approche permet de développer le modèle, de le tester et de consolider l’ergonomie en utilisant QGIS comme interface prototype avant de développer l’application web (#base-epaisse).

Le contexte étant posé, on s’intéresse dans cet article au calcul du temps de parcours qui intervient dans l’estimation des coûts d’exploitation d’une ligne.

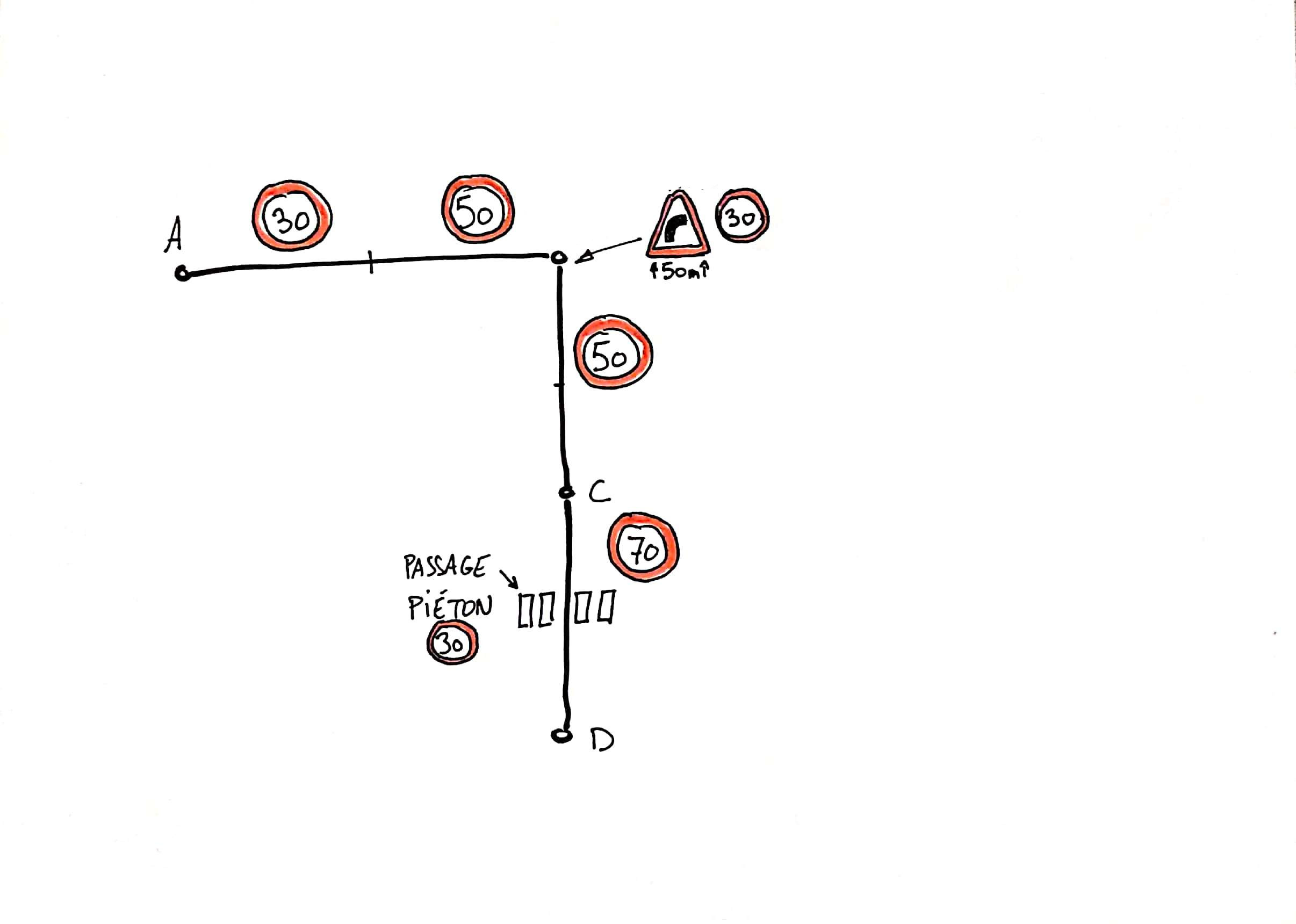
Le conducteur d’une rame choisit entre trois possibilités : accélérer, ralentir ou maintenir sa vitesse. Ce choix est soumis à plusieurs contraintes :

• les arrêts aux stations
• la vitesse maximale autorisée sur un tronçon qui est fonction de l’environnement (au milieu d’un boulevard ou dans une zone piétonne)
• la vitesse maximale en courbe
• la vitesse maximale aux carrefours et passages piétons
• les arrêts aux feux de circulation (lorsqu’ils sont rouges)

Pour déterminer le temps de parcours, il faut connaître la vitesse en tout point de la ligne. On suppose que l’accélération et la décélération sont constantes. Le problème qui se pose est donc de déterminer, sur la ligne, les zones d’accélération A, de vitesse constante O et de décélération D.

Calcul du temps de parcours dans le cas simple

Entre deux stations avec une contrainte de vitesse maximale, le conducteur accélère puis maintient sa vitesse lorsque la vitesse maximale est atteinte et enfin décélère pour s’arrêter.

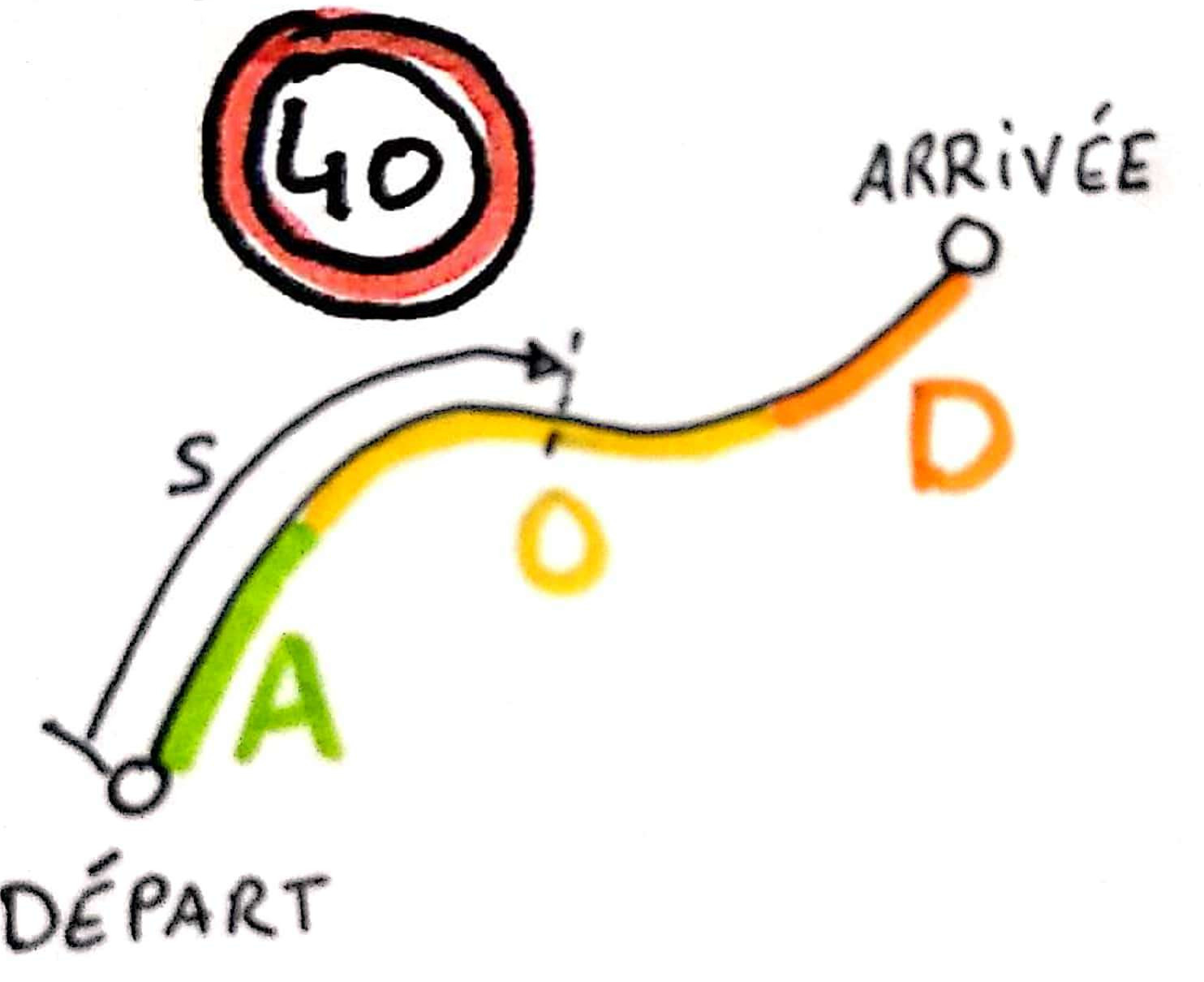
Dans le cas simple où la longueur du tronçon est suffisante pour atteindre la vitesse maximale autorisée V, le temps t_A pour attendre la vitesse maximale autorisée est V/A, la longueur s_A parcourue pendant t_A est :

s_A = At_A²/2

soit :

s_A = V²/2A

de même la distance de décélération s_D = V²/2D et la longueur parcourue à vitesse constante s_O = s_total – s_A – s_D.

Dans le cas où le tronçon n’est pas assez long pour atteindre la vitesse maximale autorisée, la vitesse maximale atteinte v est telle que v = At_A = Dt_D où t_A et t_D sont respectivement les temps d’accélération et de décélération. Pour déterminer t_A et t_D la seconde équation est la longueur totale du tronçon s_total = At_A²/2 + Dt_D²/2… t_A = sqrt(2Ds_total/(AD+A²))…

C’est presque trivial quand seuls ces deux cas sont à considérer :

• on suppose un tronçon suffisamment long pour calculer s_A et s_D,
• on vérifie que s_O est positif ou nul,
• si ce n’est pas le cas, on utilise les formules pour les tronçons courts.

Mais il y a aussi le cas où la vitesse maximale n’est pas constante entre deux stations, le cas où il faut ralentir à l’approche d’un passage piéton… Bref, beaucoup de cas particuliers et des structures conditionnelles associées.

Ça se code, mais ça manque un peu d’élégance.

Calcul du temps de parcours à partir de la courbe distance-vitesse

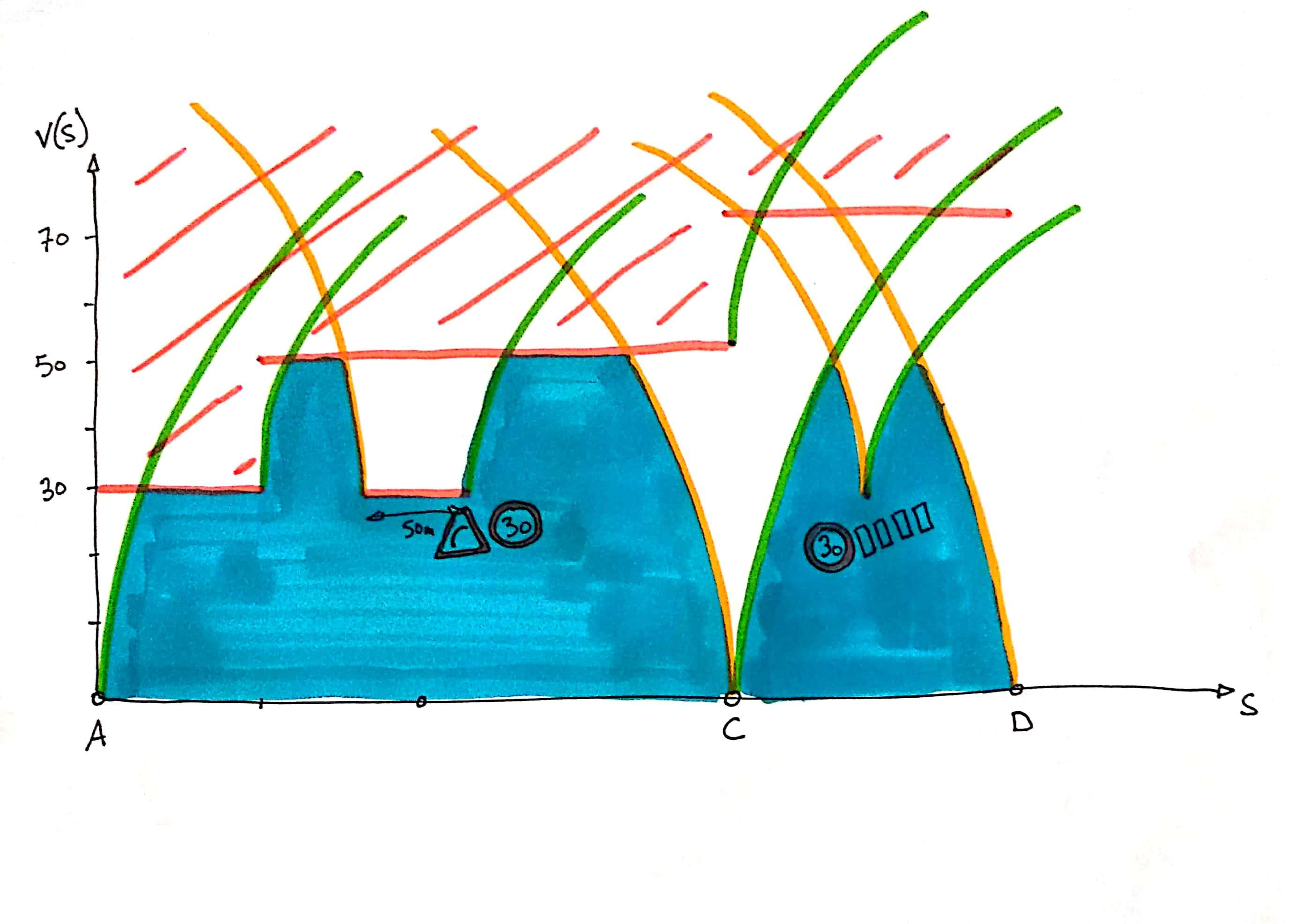
Le diagramme distance-vitesse donne la vitesse de la rame en tout point de la ligne.

Dans ce diagramme on peut positionner les stations : on connaît leurs abscisses (les distances des station à l’origine de ligne) et leurs ordonnées (une vitesse nulle).

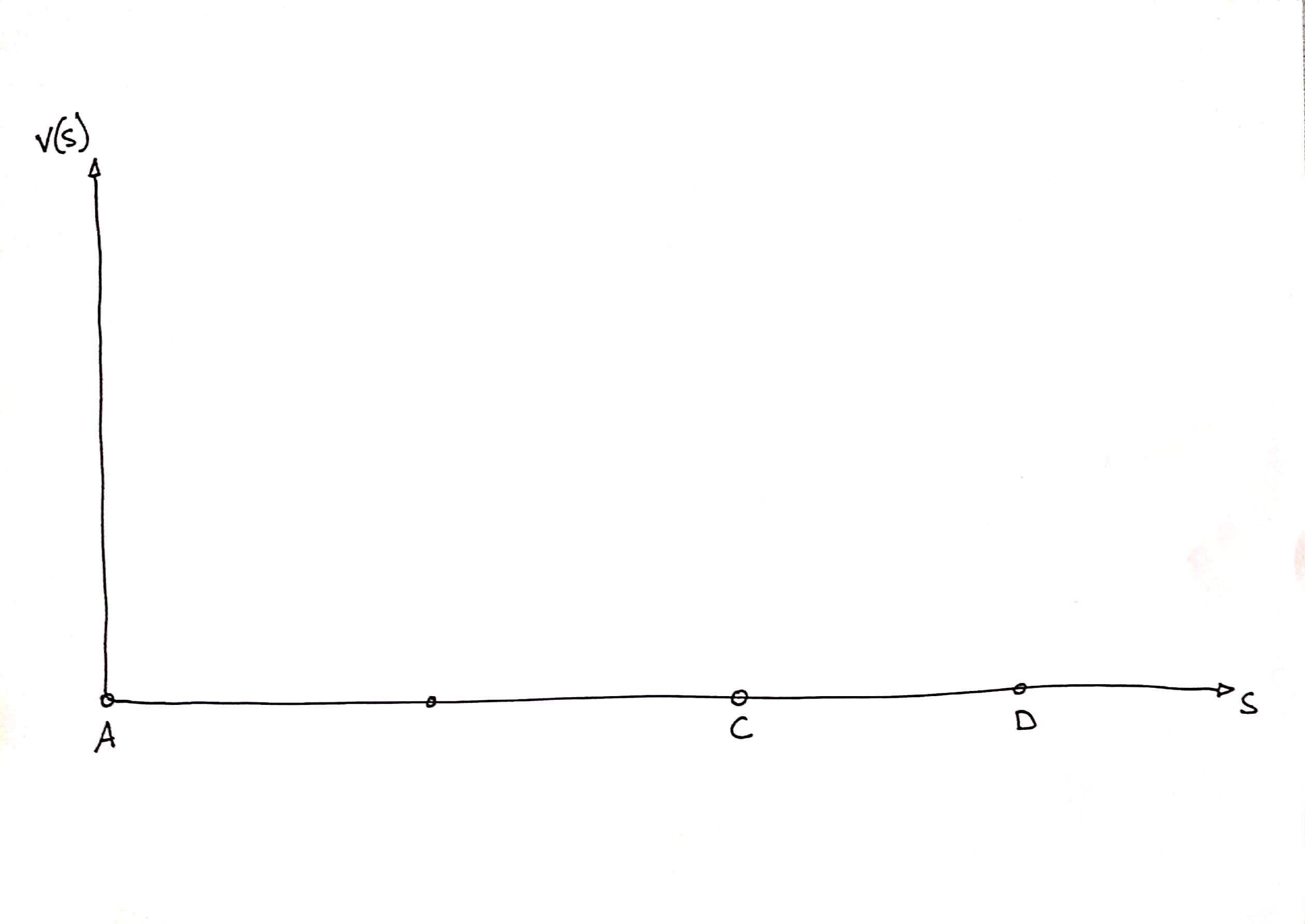
On peut aussi tracer une zone dans laquelle la courbe de vitesse ne passe pas à cause des limitations de vitesse sur les tronçons.

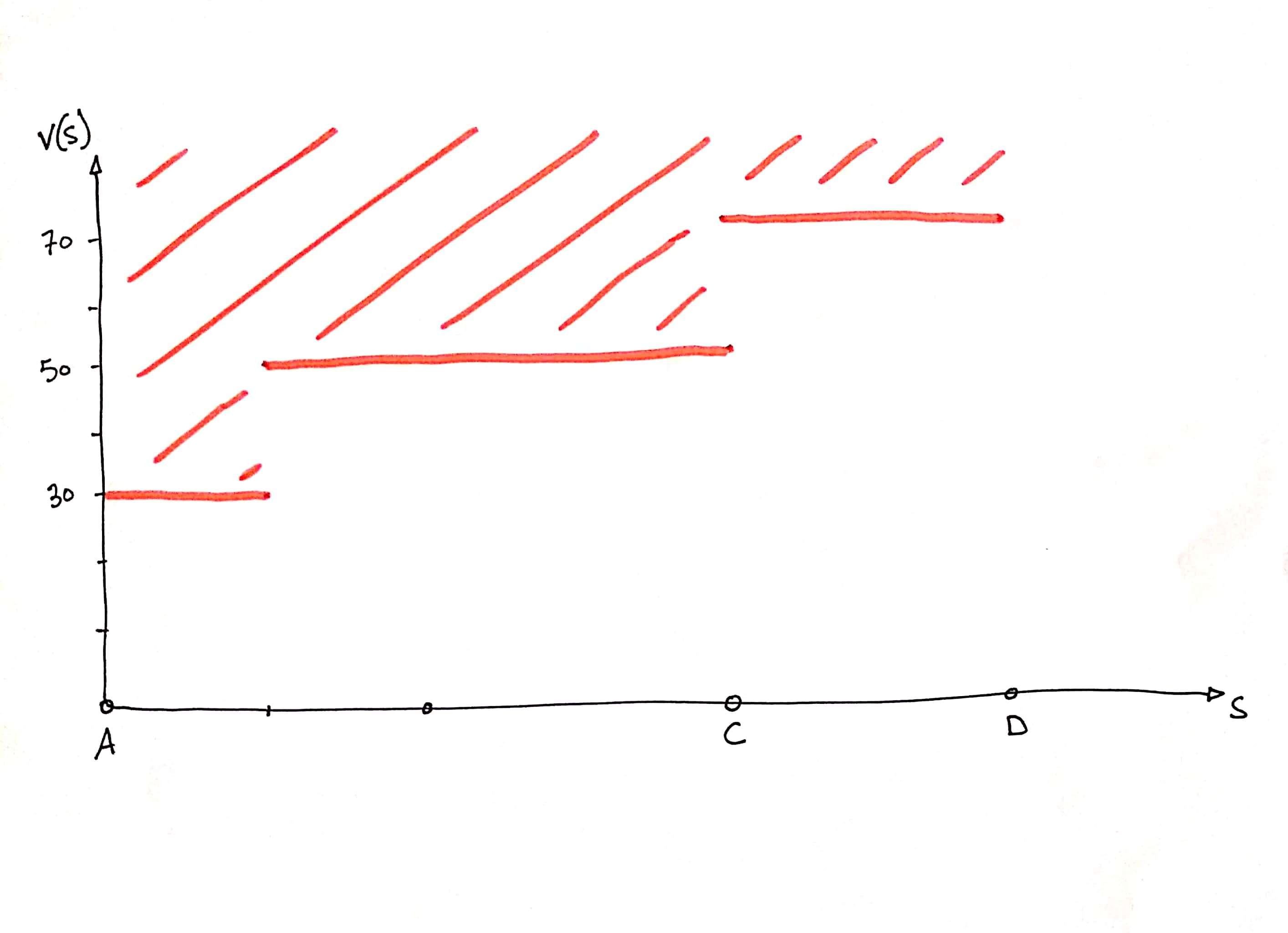
La vitesse fonction du temps, lors d’une accélération constante v(t) = At + v(0) et s(t) = At²/2 + v(0)t + s(0).

On sait tracer cette courbe avec PostGIS :

select st_makeline( st_makepoint( 0.5 * A *t^2, A*t ) ) from generate_series(0, 100, 0.5) t ;

Avec ça il suffit de tracer les accélérations et décélérations à partir des stations :

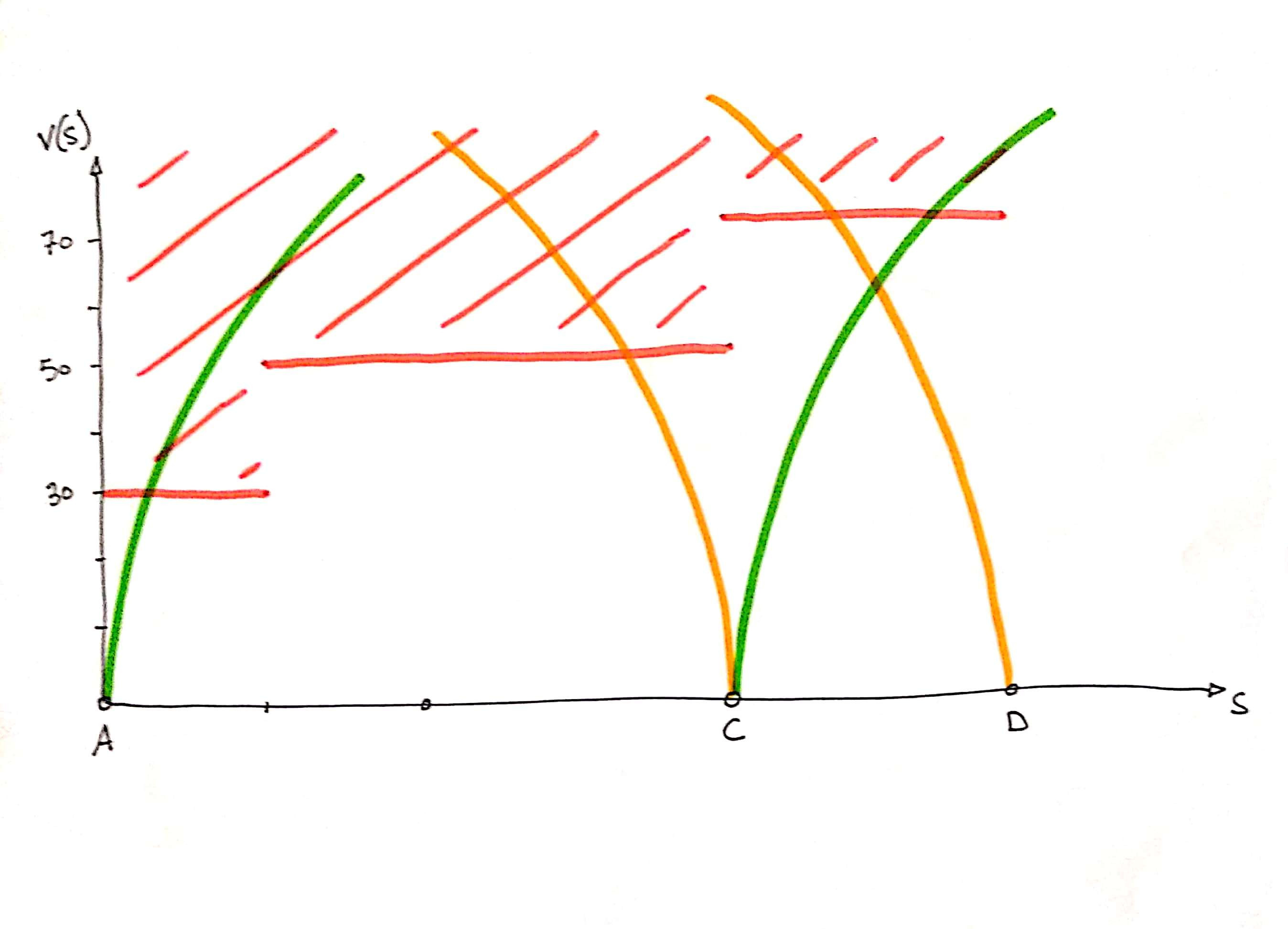
Les accélérations et décélérations liées aux changements de vitesse limite autorisés :

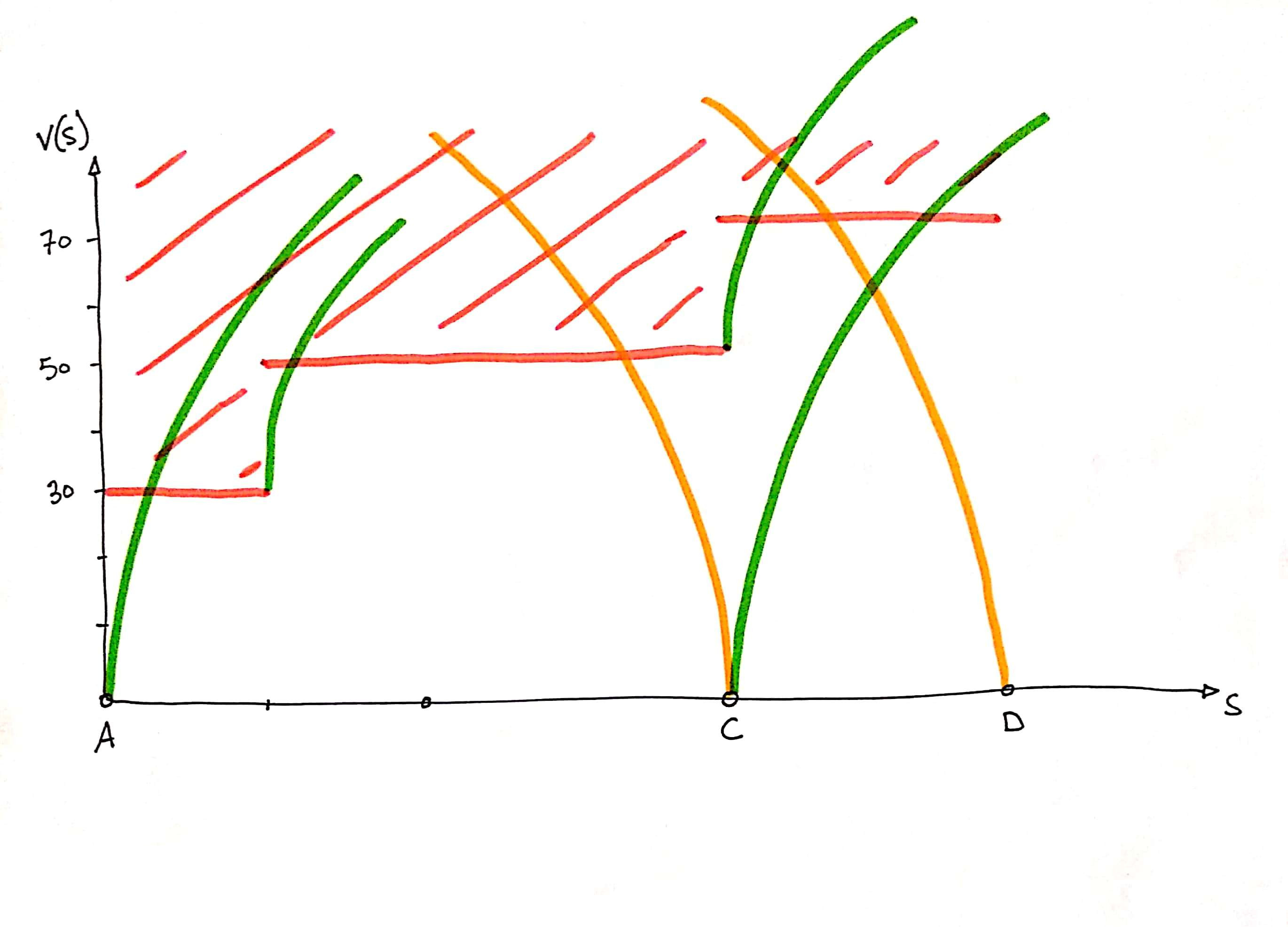
On peut facilement rajouter des points (e.g. passage piéton) des segments (e.g. courbe), où la vitesse est limitée avec l’accélération et la décélération associées :

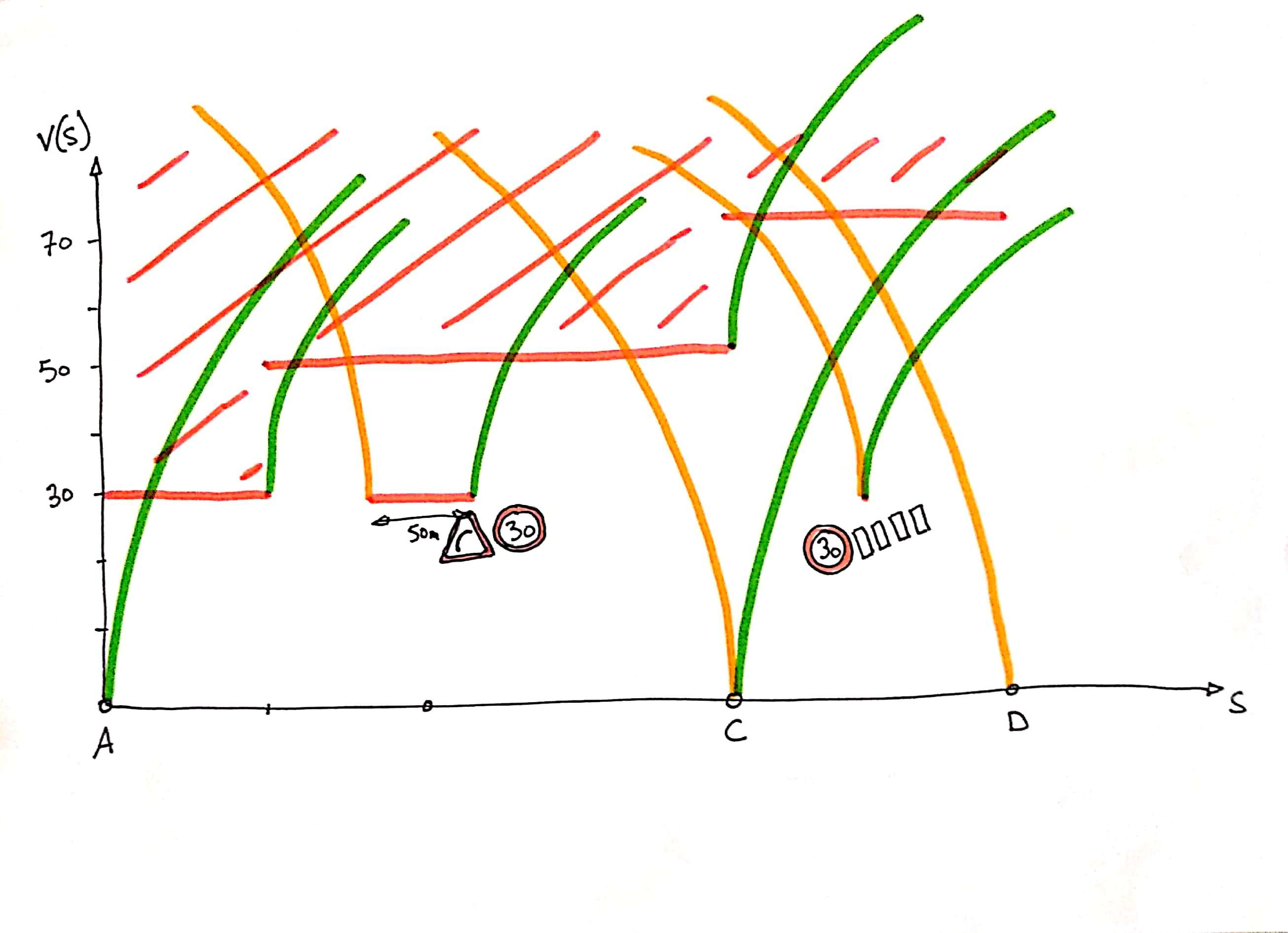
Pour extraire la courbe de vitesse à partir de cet ensemble de limites, on divise les courbes les unes par les autres, avec st_split afin d’obtenir de frontières topologiquement propres, on utilise st_polygonize pour extraire les polygones définis par ces frontières. On ne conserve que les polygones qui sont collés à l’axe des abscisses, autrement dit ceux pour qui st_length( st_intersection( polygon, axe_x ) ) > 0. La courbe distance-vitesse est l’ensemble des contours de ces polygones auxquels on soustrait l’axe des abscisses:

st_limemerge( st_difference( st_exterior_ring( polygon, axe_x ) ) )

Une fois qu’on a obtenu le courbe de distance-vitesse, on effectue une intégration numérique pour déterminer les temps de parcours.

J’espère que, comme moi, vous avez trouvé intéressant ce détournement de PostGIS qui, au-delà du stockage et du traitement d’information géographique, est un excellent outil pour faire de la géométrie.

Si vous êtes intéressés par ces sujets, n’hésitez pas à nous contacter (infos@oslandia.com)