PgRouting est une extension permettant de réaliser des calculs d’itinéraires et analyses de réseaux dans votre base de donnée géospatiale PostgreSQL.
Elle est développée en C++, à l’aide de la bibliothèque Boost Graph et dépend de l’extension PostGIS. Elle permet d’envisager des analyses de réseaux sous plusieurs angles : analyse de la structure des graphes, calcul d’itinéraires simple ou multiples, analyses d’accessibilité… L’avantage de cette bibliothèque open-source est que tous les calculs sont réalisés en base de données et donc ne nécessitent aucune installation d’outil supplémentaire. Le point commun des fonctions de routage de cette bibliothèque est d’utiliser de façon sous-jacente une notion de graphe.
PgRouting est donc une extension open source, soutenue par une communauté croissante d’individus, d’entreprises et d’organisations dont Oslandia fait partie. En effet depuis 2025, Oslandia apporte une contribution algorithmique à cette extension. Sa première contribution a porté sur l’ajout à l’extension de la fonction pgr_contractionHierarchies. A l’occasion de cette contribution, nous vous proposons une présentation des principales fonctionnalités de PgRouting, afin de pouvoir prendre rapidement en main cette bibliothèque.
Qu’est-ce qu’un graphe ?
Un graphe est une structure de données complexe composée de nœuds et d’arcs, les arcs reliant les nœuds entre eux.
Exemple de graphe composé de :
- 6 noeuds (a, b, c, d, e et f) ;
- 9 arcs (a->b, a->c, a->e, b->d, c->d, c->f, d->b, e->b, f->d).
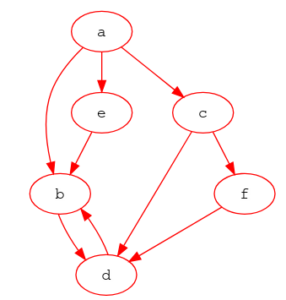
Des coûts ou des capacités peuvent ensuite être attribués aux arcs ou aux noeuds pour représenter différentes situations concrètes. Ce type de structure de données se prête naturellement à la modélisation de problématiques de calcul d’itinéraires, d’optimisation de l’écoulement de flux, de minimisation des coûts de construction d’un réseau électrique, de télécommunication ou d’eau potable, de détermination des points de vulnérabilité d’un réseau…
Les graphes utilisés dans PgRouting peuvent être orientés ou non et basés ou non sur des géométries. Des coûts et capacités statiques, c’est-à-dire considérés comme invariants dans le temps, peuvent être attribués aux arcs.
Les fonctions de PgRouting
Cette extension de PostgreSQL est dédiée aux calculs en temps non-contraint sur des graphes, donc plutôt à des fins d’analyse de réseaux ou d’aide à la décision hors-ligne. Un de ses atouts principaux est sa simplicité d’utilisation, qui est celle du SQL.
PgRouting propose une grande variété de fonctions qui travaillent sur les graphes. Elles sont taguées en fonction de leur niveau de maturité :
- ✅ les fonctions officielles ;
- 🚧 les fonctions proposées ;
- 🧪 les fonctions expérimentales.
Nous vous proposons dans cet article de vous présenter les fonctions officielles de cette bibliothèque.
Préparer le graphe
Création d’une topologie
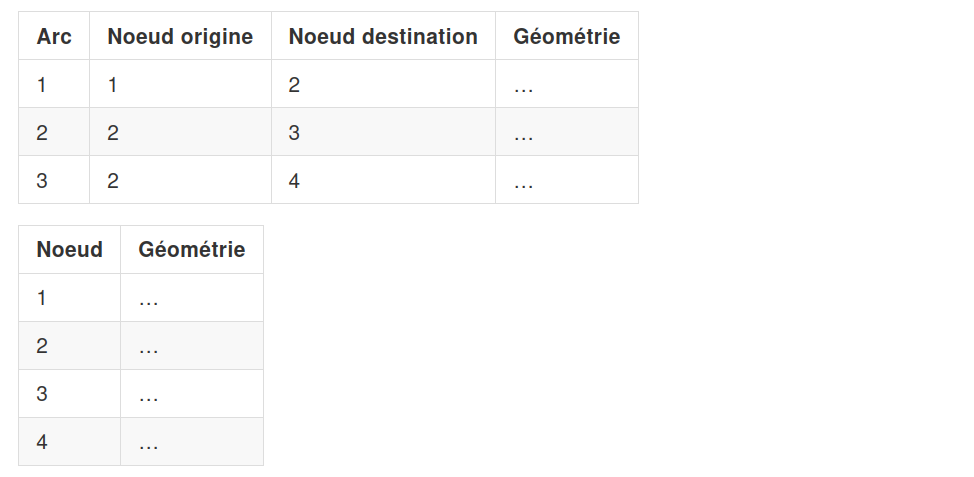
Il est possible, grâce à PgRouting, de construire une topologie à partir d’une table d’objets linéaires représentant les arcs d’un réseau. Il s’agit plus exactement de créer et remplir les deux tables ci-dessous, qui constituent une structure de graphe : les arcs et les noeuds.
Cette fonction sait tenir compte d’éventuels écarts entre les extrémités des polylignes qui composent le réseau, comme l’illustrent les deux figures ci-dessous.
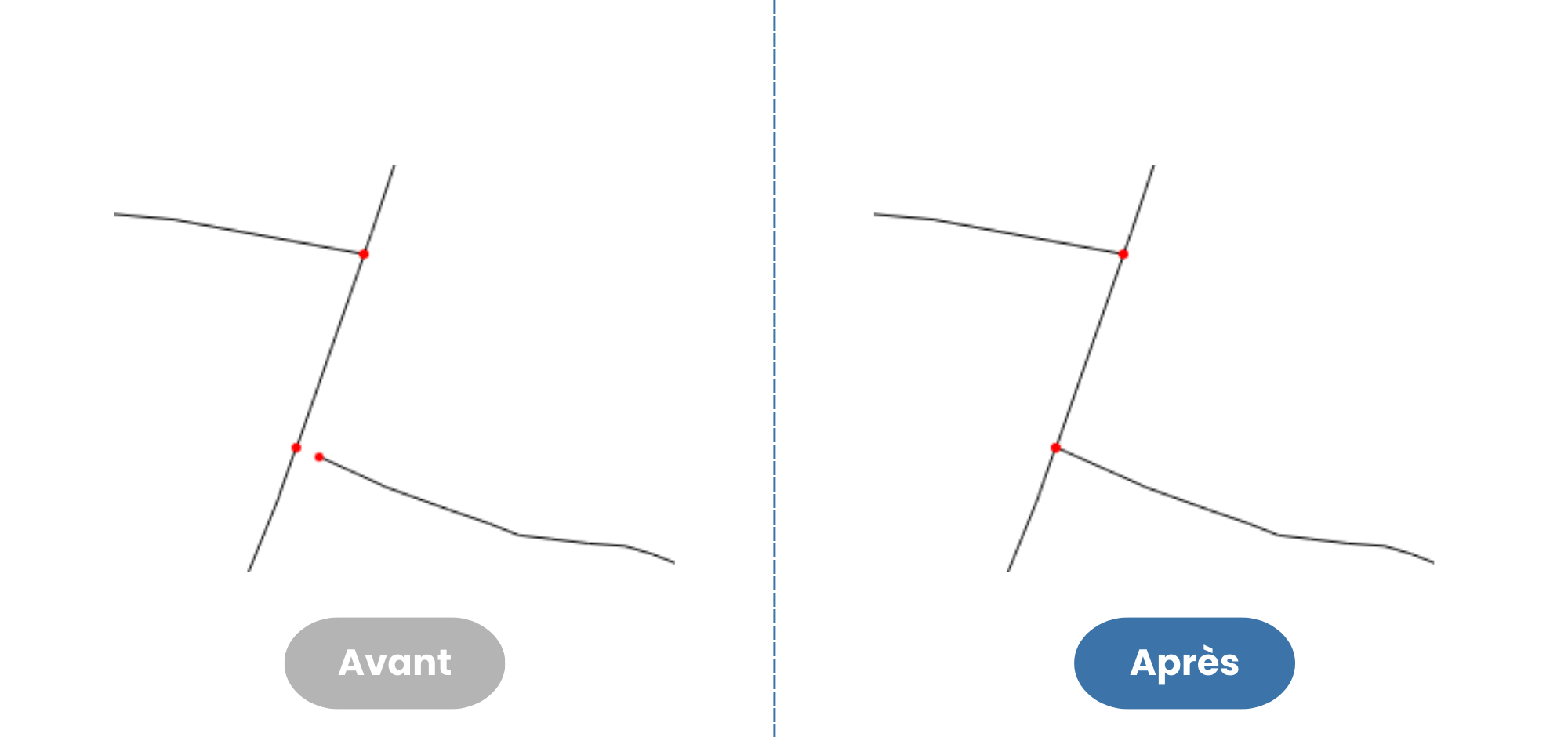Si on dispose de noeuds additionnels, non-connectés au graphe (par exemple des points d’intérêt le long d’un graphe routier), il existe également une fonction pour les reprojeter sur les arcs du graphe situés dans un rayon donné.
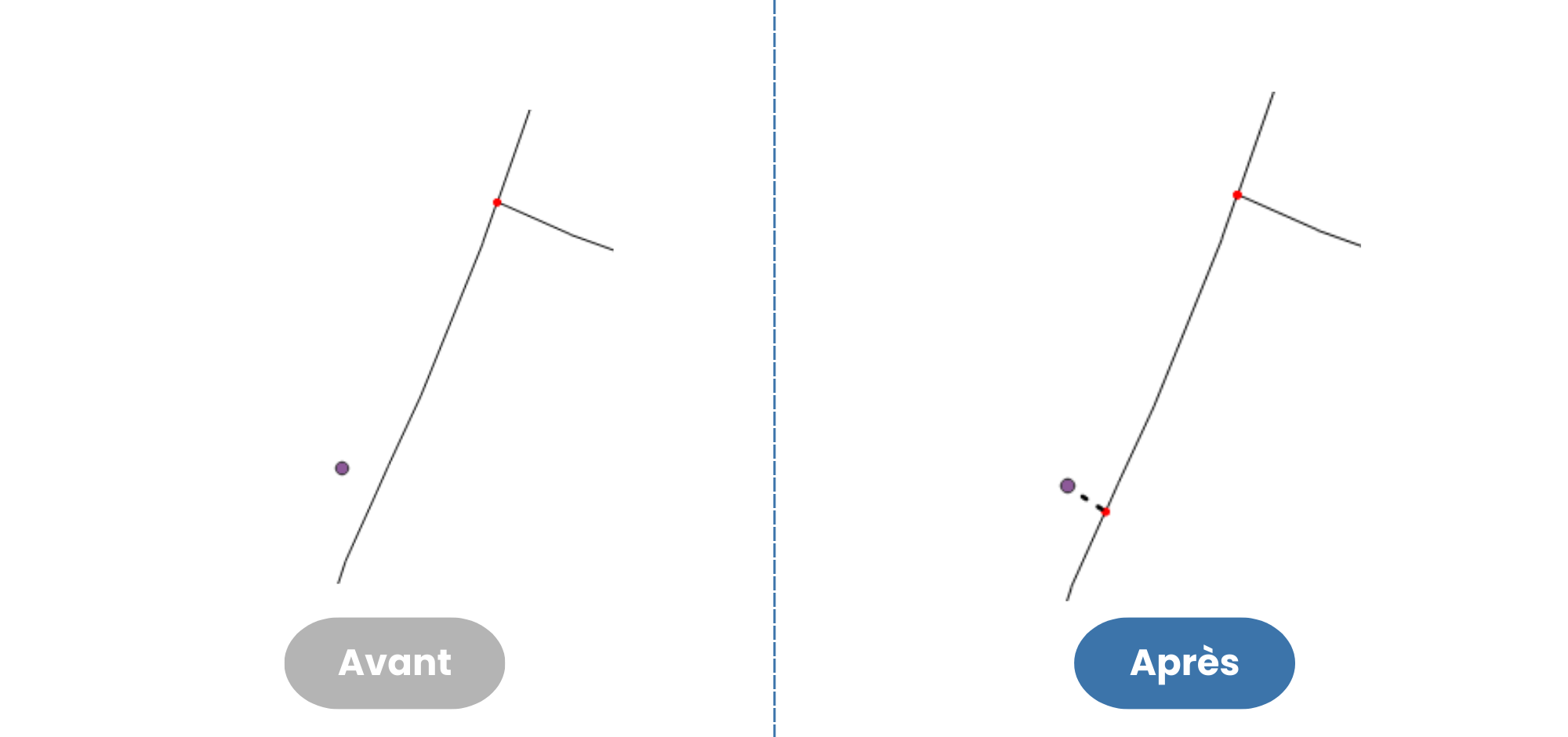Lorsque le graphe dispose d’une géométrie pour les arcs, il est également possible de vérifier si ces géométries se croisent ou se touchent. Si tel est le cas, une fonction PgRouting propose de redécouper les géométries des arcs pour insérer un nouveau noeud à chaque croisement ou point de contact.
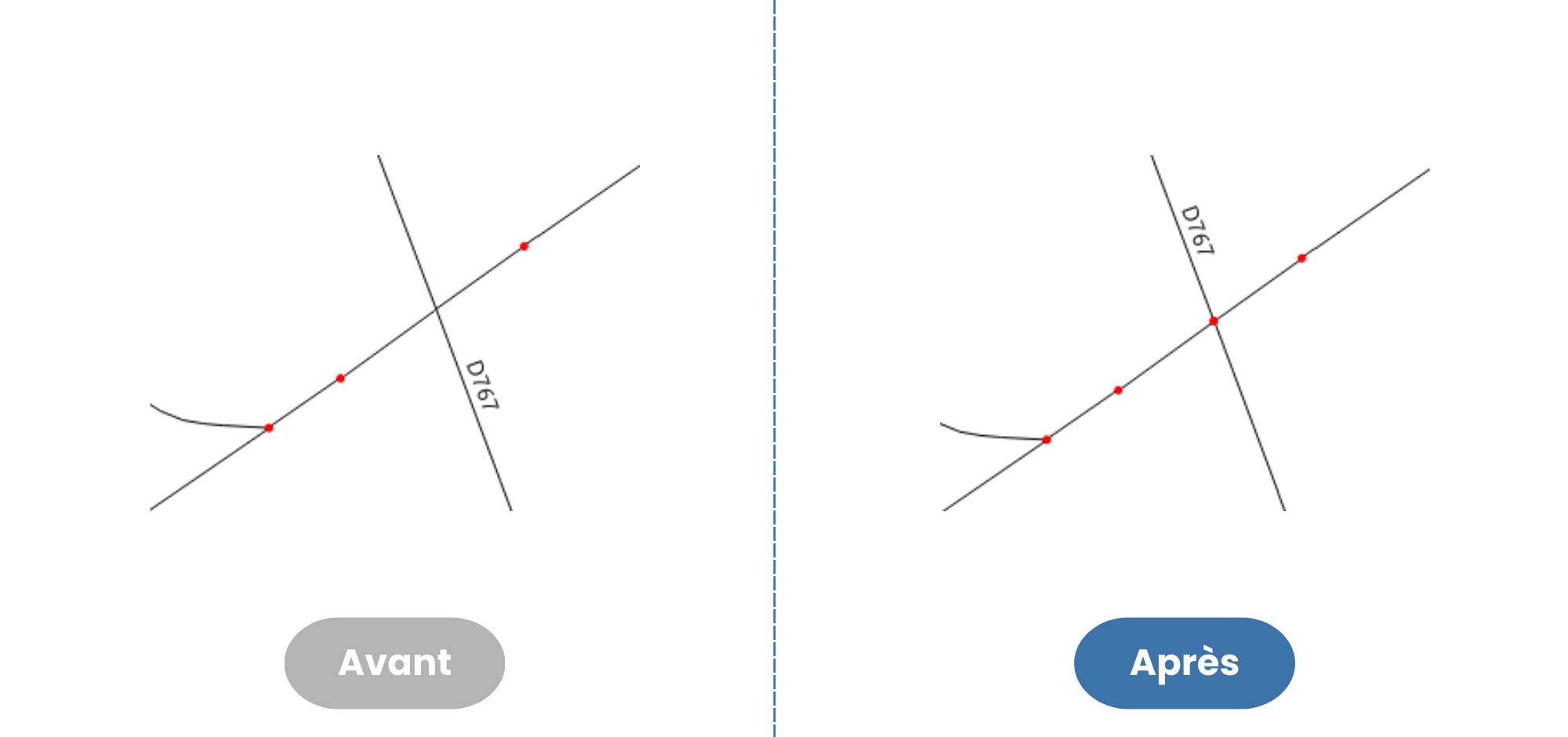
L’application d’une telle fonction suppose, dans le cas d’un réseau routier, qu’on sait extraire du graphe un réseau non-dénivelé (sans pont ni passage sous-terrain), dans lequel les intersections des géométries des arcs correspondent donc à des intersections réelles.
Pour quoi faire ?
Préparer ses données pour un calcul de graphe
Corriger le graphe
Degrés des noeuds
Une fois le graphe construit, PgRouting permet de calculer les degrés des noeuds du graphe.
Pour quoi faire ?
Il s’agit ici de qualifier le graphe, détecter des erreurs et les corriger pour préparer les calculs. Les degrés des noeuds permettent notamment de détecter d’éventuelles incohérences de sens de circulation sur un réseau routier ou des arcs isolés.
Analyse de connexité
PgRouting permet de détecter les composantes connexes d’un graphe orienté (on parle alors de composantes *fortement connexes*) ou non-orienté.
Une fonction est également proposée pour détecter les composantes biconnectées. Une composante biconnectée est telle que le retrait d’un noeud de cette composante la déconnecte du reste du graphe. Une deuxième fonction, avec une signature différente, retourne uniquement les noeuds d’articulation, qui relient les composantes biconnectées entre elles. Une troisième fonction retourne les *ponts*, c’est-à-dire les arcs dont le retrait augmente le nombre de composantes connexes du graphe.
Pour quoi faire ?
Détecter des défauts de connexité dans les données et les corriger pour les préparer à un calcul de graphe
Lancer des calculs sur le graphe
Calcul de chemins optimaux
Les fonctions de calcul de chemins optimaux disponibles dans PgRouting sont très diverses et ont différentes signatures. Certaines fonctions retournent en sortie des coûts par paire origine-destination. D’autres retournent en sortie des chemins complets, sous différentes formes :
- chemins optimaux ;
- iso-distances ;
- k plus courts chemins ;
- chemins optimaux avec restriction de mouvements tournants.
Ces signatures de fonctions sont utilisées par différents algorithmes. Ces croisements entre signatures et algorithmes actuellement disponibles dans PgRouting sont résumés dans le tableau ci-dessous :
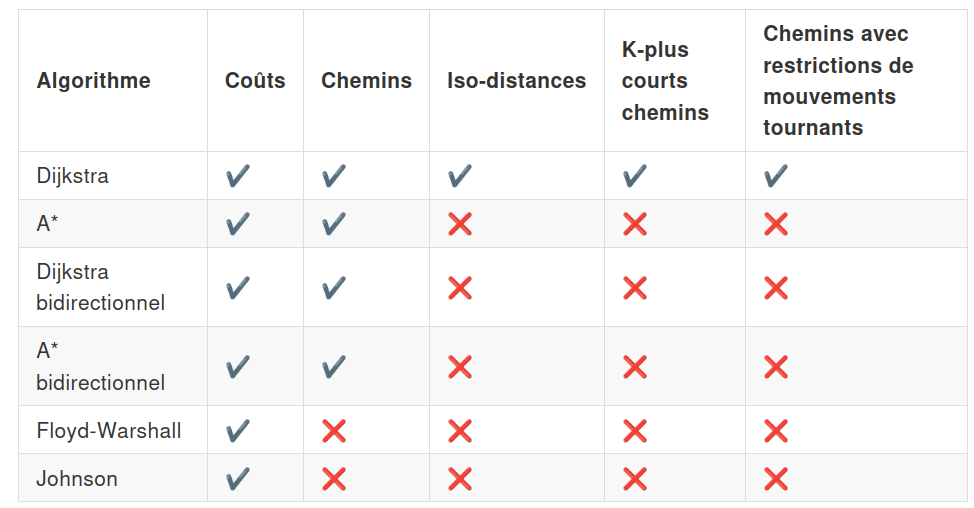
Ces fonctions offrent de bonnes performances de calcul hors-ligne avec un graphe statique, grâce à la variété des signatures de fonctions qui permettent de lancer plusieurs calculs de chemin sur un même graphe. En revanche, dès que les caractéristiques du graphe changent, il est nécessaire de relancer un nouvel appel de fonction, donc une nouvelle construction d’un graphe en mémoire, ce qui dégrade les performances et rend cette bibliothèque un peu moins pertinente pour un usage en temps réel ou sur des graphes aux caractéristiques dynamiques et de grande taille.
Pour quoi faire ?
Optimisation d’itinéraires pour préparer des livraisons, des interventions (médecins, pompiers, etc.)…
Arbres couvrants de poids minimal
PgRouting propose également des algorithmes de construction d’arbres couvrants de poids minimal.
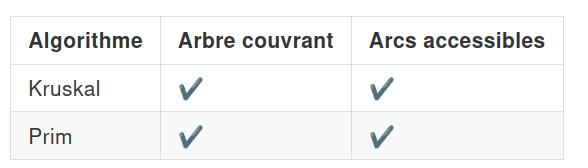
Pour quoi faire ?
Déterminer une configuration qui minimise le coût de construction d’un réseau desservant des habitations (eau, électricité, télécom)…
Ecoulement de flot maximal
Les algorithmes de flot maximal peuvent par exemple être utilisés pour modéliser les capacités d’écoulement dans un réseau. Il s’agit de déterminer une quantité maximale qu’on peut faire passer par période entre deux noeuds d’un réseau donné, auquel on a au préalable attribué des capacités arc par arc. Dans ce cas, le parcours des arcs ne se voit pas attribuer de coûts.
Les fonctions PgRouting retournent soit la valeur maximale du flot pouvant s’écouler par période, soit un détail des volumes affectés arc par arc et de la capacité résiduelle.
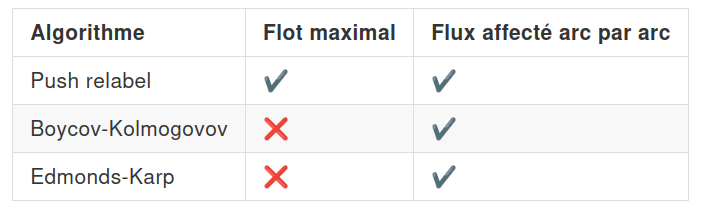
Pour quoi faire ?
Déterminer la capacité d’un réseau d’écoulement d’eau…
Problème du voyageur de commerce
Des fonctions sont proposées pour résoudre le problème du voyageur de commerce, qui consiste à trouver une tournée de coût minimal desservant *n* villes, à partir d’une matrice des coûts de parcours des distances séparant chaque couple de villes.
PgRouting ne propose pas de résolution exacte de ce problème dans le cas général, en raison de sa complexité de résolution, mais une fonction qui garantit de trouver une solution pas trop mauvaise, c’est-à-dire de coût inférieur au double du coût d’une solution optimale.
Une variante générant une solution exacte est également proposée pour le cas où le coût entre les noeuds correspond à la distance euclidienne qui les sépare.
Les fonctions retournent la séquence des villes parcourues et une agrégation des coûts.
Pour quoi faire ?
La résolution de ce type de problèmes permet d’optimiser des tournées pour des véhicules de livraison entre des points bien identifiés du territoire.
En complément à PgRouting, PostgreSQL offre de façon native des possibilités pour faire des calculs sur des réseaux, en particulier des calculs de chemins. Il s’agit des requêtes récursives, appelées Recursive Common Table Expressions. On peut facilement à l’aide de ce type de requête parcourir un graphe. Les index sont très importants dans ce contexte pour obtenir de bonnes performances.
Si vous avez apprécié cet article, que vous avez appris des choses mais que vous auriez envie d’en apprendre encore plus sur le sujet du routing, sachez qu’Oslandia est contributeur de PgRouting, mais propose également une formation sur le routing.
Vous avez des questions ? Contactez-nous !
